Common LUT Format (CLF) - A Common File Format for Look-Up Tables

Introduction

Look-Up Tables (LUTs) are a common implementation for transformations from one set of color values to another. With a large number of product developers providing software and hardware solutions for LUTs, there is an explosion of unique vendor-specific LUT file formats, which are often only trivially different from each other. This can create workflow problems when a LUT being used on a production is not supported by one or more of the applications being used. Furthermore, many LUT formats are designed for a particular use case only and lack the quality, flexibility, and metadata needed to meet modern requirements.

The Common LUT Format (CLF) can communicate an arbitrary chain of color operators (also called processing nodes) which are sequentially processed to achieve an end result. The set of available operator types includes matrices, 1D LUTs, 3D LUTs, ASC-CDL, log and exponential shaper functions, and more. Even when 1D or 3D LUTs are not present, CLF can be used to encapsulate any supported color transforms as a text file conforming to the XML schema.

Scope

This document introduces a human-readable text file format for the interchange of color transformations using an XML schema. The XML format supports Look-Up Tables of several types: 1D LUTs, 3D LUTs, and 3×1D LUTs, as well as additional transformation needs such as matrices, range rescaling, and “shaper LUTs.” The document defines what is a valid CLF file. Though it is not intended as a tutorial for users to create their own files, LUT creators will find it useful to understand the elements and attributes available for use in a CLF file. The document is also not intended to provide guidance to implementors on how to optimize their implementations, but does provide a few notes on the subject. This document assumes the reader has knowledge of basic color transformation operators and XML.

References

The following standards, specifications, articles, presentations, and texts are referenced in this text:

• IETF RFC 3066: IETF (Internet Engineering Task Force). RFC 3066: Tags for the Identification of Lan- guages, ed. H. Alvestrand. 2001 IEEE DRAFT Standard P123
• Academy S-2014-002, Academy Color Encoding System – Versioning System
• Academy TB-2014-002, Academy Color Encoding System Version 1.0 User Experience Guidelines
• ASC Color Decision List (ASC CDL) Transfer Functions and Interchange Syntax. ASC-CDL Release1.2. Joshua Pines and David Reisner. 2009-05-04.

Specification

General

A Common LUT Format (CLF) file shall be written using Extensible Markup Language (XML) and adhere to a defined XML structure. A CLF file shall have the file extension '.clf'.

The top level element in a CLF file defines a ProcessList which represents a sequential set of color transformations. The result of each individual color transformation feeds into the next transform in the list to create a daisy chain of transforms.

An application reads a CLF file and initializes a transform engine to perform the operations in the list. The transform engine reads as input a stream of code values of pixels, performs the calculations and/or interpolations, and writes an output stream representing a new set of code values for the pixels.

In the sequence of transformations described by a ProcessList, each ProcessNode performs a transform on a stream of pixel data, and only one input line (input pixel values) may enter a node and only one output line (output pixel values) may exit a node. A ProcessList may be defined to work on either 1- component or 3-component pixel data, however all transforms in the list must be appropriate, especially in the 1-component case (black-and-white) where only 1D LUT operations are allowed. Implementation may process 1-component transforms by applying the same processing to R, G, and B.

Figure 1. Example of a ProcessList containing a sequence of multiple ProcessNodes

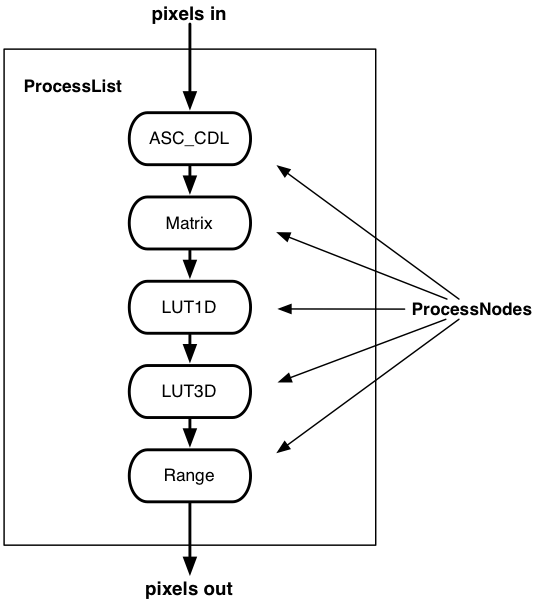
The file format does not provide a mechanism to assign color transforms to either image sequences or image regions. However, the XML structure defining the LUT transform, a ProcessList, may be encapsulated in a larger XML structure potentially providing that mechanism. This mechanism is beyond the scope of this document.

Each CLF file shall be completely self-contained requiring no external information or metadata. The full content of a color transform must be included in each file and a color transform may not be incorporated by reference to another CLF file. This restriction ensures that each CLF file can be an independent archival element.

Each ProcessList shall be given a unique ID for reference.

The data for LUTs shall be an ordered array that is either all floats or all integers. When three RGB color components are present, it is assumed that these are red, green, and blue in that order. There is only one order for how the data array elements are specified in a LUT, which is in general from black to white (from the minimum input value position to the maximum input value position). Arbitrary ordering of list elements is not supported in the format (see XML Elements for details).

Note

For 3D LUTs, the indexes to the cube are assumed to have regular spacing across the range of input values. To accommodate irregular spacing, a "halfDomain" 1D LUT or Log node should be used as a shaper function prior to the 3D LUT.

XML Structure

General

A CLF file shall contain a single occurrence of the XML root element known as the ProcessList. The ProcessList element shall contain one or more elements known as ProcessNodes. The order and number of process nodes is determined by the designer of the CLF file.

An example of the overall structure of a simple CLF file is thus:

<ProcessList id="123">
    <Matrix id="1">
        data & metadata
    </Matrix>
    <LUT1D id="2">
        data & metadata
    </LUT1D> 
    <Matrix id="3">
        data & metadata
    </Matrix>
</ProcessList>

XML Version and Encoding

A CLF file shall include a starting line that declares XML version number and character encoding. This line is mandatory once in a file and looks like this:

<?xml version="1.0" encoding="UTF-8"?>

Comments

The file may also contain XML comments that may be used to describe the structure of the file or save information that would not normally be exposed to a database or to a user. XML comments are enclosed in brackets like so:

<!--  This is a comment  -->

Language

It is often useful to identify the natural or formal language in which text strings of XML documents are written. The special attribute named xml:lang may be inserted in XML documents to specify the language used in the contents and attribute values of any element in an XML document. The values of the attribute are language identifiers as defined by IETF RFC 3066. In addition, the empty string may be specified. The language specified by xml:lang applies to the element where it is specified (including the values of its attributes), and to all elements in its content unless overridden with another instance of xml:lang. In particular, the empty value of xml:lang can be used to override a specification of xml:lang on an enclosing element, without specifying another language.

White Space

Particularly when creating CLF files containing certain elements (such as Array, LUT1D, or LUT3D) it is desirable that single lines per entry are maintained so that file contents can be scanned more easily by a human reader. There exist some difficulties with maintaining this behavior as XML has some non-specific methods for handling white-space. Especially if files are re-written from an XML parser, white space will not necessarily be maintained. To maintain line layout, XML style sheets may be used for reviewing and checking the CLF file’s entries.

Newline Control Characters

Different end of line conventions, including <CR>, <LF>, and <CRLF>, are utilized between Mac, Unix, and Windows systems. Different newline characters may result in the collapse of values into one long line of text. To maintain intended linebreaks, CLF specifies that the ‘newline’ string (i.e. the byte(s) to be interpreted as ending each line of text) shall be the single code value \(10_{10} = 0\textrm{A}_{16}\) (ASCII ‘Line Feed’ character), also indicated <LF>.

Note

Parsers of CLF files may choose to interpret Microsoft’s <CR><LF> or older-MacOS’ <CR> newline conventions, but CLF files should only be generated with the <LF> encoding.

Note

<LF> is the newline convention native to all *nix operating systems (including Linux and modern macOS).

XML Elements

Figure 2. Object Model of XML Elements

ProcessList

Description:
The ProcessList is the root element for any CLF file and is composed of one or more ProcessNodes. A ProcessList is required even if only one ProcessNode will be present.

Note

The last node of the ProcessList is expected to be the final output of the LUT. A LUT designer can allow floating-point values to be interpreted by applications and thus delay control of the final encoding through user selections.

Note

If needed, a Range node can be placed at the end of a ProcessList to control minimum and maximum output values and clamping.

Attributes:

id (required)

a string to serve as a unique identifier of the ProcessList

compCLFversion (required)

a string indicating the minimum compatible CLF specification version required to read this file
The compCLFversion corresponding to this version of the specification is be "3.0".

name (optional)

a concise string used as a text name of the ProcessList for display or selection from an application’s user interface

inverseOf (optional)

a string for linking to another ProcessList id (unique) which is the inverse of this one

Elements:

Description (optional)

a string for comments describing the function, usage, or any notes about the ProcessList. A ProcessList can contain zero or more Description elements.

InputDescriptor (optional)

an arbitrary string used to describe the intended source code values of the ProcessList

OutputDescriptor (optional)

an arbitrary string used to describe the intended output target of the ProcessList (e.g. target display)

ProcessNode (required)

a generic XML element that in practice is substituted with a particular color operator. The ProcessList must contain at least one ProcessNode. The ProcessNode is described in ProcessNode.

Info (optional)

optional element for including additional custom metadata not needed to interpret the transforms. The Info element includes:

AppRelease (optional)

a string used for indicating application software release level

Copyright (optional)

a string containing a copyright notice for authorship of the CLF file

Revision (optional)

a string used to track the version of the LUT itself (e.g. an increased resolution from a previous version of the LUT)

ACEStransformID (optional)

a string containing an ACES transform identifier as described in Academy S-2014-002. If the transform described by the ProcessList is the concatenation of several ACES transforms, this element may contain several ACES Transform IDs, separated by white space or line separators. This element is mandatory for ACES transforms and may be referenced from ACES Metadata Files.

ACESuserName (optional)

a string containing the user-friendly name recommended for use in product user interfaces as described in Academy TB-2014-002

CalibrationInfo (optional)

container element for calibration metadata used when making a LUT for a specific device.
CalibrationInfo can contain the following child elements:

DisplayDeviceSerialNum
DisplayDeviceHostName
OperatorName
CalibrationDateTime
MeasurementProbe
CalibrationSoftwareName
CalibrationSoftwareVersion

ProcessNode

Description:
A ProcessNode element represents an operation to be applied to the image data. At least one ProcessNode element must be included in a ProcessList. The generic ProcessNode element contains attributes and elements that are common to and inherited by the specific sub-types of the ProcessNode element that can substitute for ProcessNode. All ProcessNode substitutes shall inherit the following attributes.

Attributes:

id (optional)

a unique identifier for the ProcessNode

name (optional)

a concise string defining a name for the ProcessNode that can be used by an application for display in a user interface

inBitDepth (required)

a string that is used by some ProcessNodes to indicate how array or parameter values have been scaled

outBitDepth (required)

a string that is used by some ProcessNodes to indicate how array or parameter values have been scaled The supported values for both inBitDepth and outBitDepth are the same:

• "8i": 8-bit unsigned integer
• "10i": 10-bit unsigned integer
• "12i": 12-bit unsigned integer
• "16i": 16-bit unsigned integer
• "16f": 16-bit floating point (half-float)
• "32f": 32-bit floating point (single precision)

Elements:

Description (optional)

an arbitrary string for describing the function, usage, or notes about the ProcessNode. A ProcessNode can contain one or more Descriptions.

Array

Description:
The Array element contains a table of entries with a single line for each grouping of values. This element is used in the LUT1D, LUT3D, and Matrix ProcessNodes. The dim attribute specifies the dimensions of the array and, depending on context, defines the size of a matrix or the length of a LUT table. The specific formatting of the dim attribute must match with the type of node in which it is being used. The usages are summarized below but specific requirements for each application of Array are described when it appears as a child element for a particular ProcessNode.

Attributes:

dim (required)

Specifies the dimension of the LUT or the matrix and the number of color components. The dim attribute provides the dimensionality of the indexes, where:

• 4 entries represent the dimensions of a 3D cube and the number of components per entry.
  e.g. dim = 17 17 17 3 indicates a 17-cubed 3D LUT with 3 color components

• 2 entries represent the dimensions of a matrix.
  e.g. dim = 3 3 indicates a 3×3 matrix
  e.g. dim = 3 4 indicates a 3×4 matrix

• 2 entries represent the length of the LUT and the component value (1 or 3).
  e.g. dim = 256 3 indicates a 256 element 1D LUT with 3 components (a 3×1D LUT)
  e.g. dim = 256 1 indicates a 256 element 1D LUT with 1 component (1D LUT)

Substitutes for ProcessNode

General

The attributes and elements defined for ProcessNode are inherited by the substitutes for ProcessNode. This section defines the available substitutes for the generalized ProcessNode element.

The inBitDepth of a ProcessNode must match the outBitDepth of the preceding ProcessNode (if any).

LUT1D

Description:
A 1D LUT transform uses an input pixel value, finds the two nearest index positions in the LUT, and then interpolates the output value using the entries associated with those positions.

This node shall contain either a 1D LUT or a 3x1D LUT in the form of an Array. If the input to a LUT1D is an RGB value, the same LUT shall be applied to all three color components.

A 3x1D LUT transform looks up each color component in a separate LUT1D of the same length. In a 3x1D LUT, by convention, the LUT1D for the first component goes in the first column of Array.

The scaling of the array values is based on the outBitDepth (the inBitDepth is not considered).

The length of a 1D LUT should be limited to at most 65536 entries, and implementations are not required to support LUT1Ds longer than 65536 entries.

Linear interpolation shall be used for LUT1D. More information about linear interpolation can be found in Appendix A.

Elements:

Array (required)

an array of numeric values that are the output values of the 1D LUT. Array shall contain the table entries of a LUT in order from minimum value to maximum value.

For a 1D LUT, one value per entry is used for all color channels. For a 3x1D LUT, each line should contain 3 values, creating a table where each column defines a 1D LUT for each color component.

For RGB, the first column shall correspond to R’s 1D LUT, the second column shall correspond to G’s 1D LUT, and the third column shall correspond to B’s 1D LUT.

Attributes:

dim (required)

two integers that represent the dimensions of the array. The first value defines the length of the array and shall equal the number of entries (lines) in the LUT. The second value indicates the number of components per entry and shall equal 1 for a 1D LUT or 3 for a 3x1D LUT.

Example

dim = "1024 3" indicates a 1024 element 1D LUT with 3 component color (a 3x1D LUT)

Example

dim = "256 1" indicates a 256 element 1D LUT with 1 component color (a 1D LUT)

Note

Array is formatted differently when it is contained in a LUT3D or Matrix element (see Array).

Attributes:

interpolation (optional)

a string indicating the preferred algorithm used to interpolate values in the 1DLUT. This attribute is optional but, if present, shall be set to "linear".

Note

Previous versions of this specification allowed for implementations to utilize different types of interpolation but did not define what those interpolation types were or how they should be labeled. For simplicity and to ensure similarity across implementations, 1D LUT interpolation has been limited to "linear" in this version of the specification. Support for additional interpolation types could be added in future version.

halfDomain (optional)

If this attribute is present, its value must equal “true”. When true, the input domain to the node is considered to be all possible 16-bit floating-point values, and there must be exactly 65536 entries in the Array element.

Note

For example, the unsigned integer 15360 has the same bit-pattern (0011110000000000) as the half-float value 1.0, so the 15360th entry (zero-indexed) in the Array element is the output value corresponding to an input value of 1.0.

rawHalfs (optional)

If this attribute is present, its value must equal “true”. When true, the rawHalfs attribute indicates that the output array values in the form of unsigned 16-bit integers are interpreted as the equivalent bit pattern, half floating-point values.

Note

For example, to represent the value 1.0, one would use the integer 15360 in the Array element because it has the same bit-pattern. This allows the specification of exact half-float values without relying on conversion from decimal text strings.

Examples:

<LUT1D id="lut-23" name="4 Value Lut" inBitDepth="12i" outBitDepth="12i"> 
    <Description>1D LUT - Turn 4 grey levels into 4 inverted codes</Description>
    <Array dim="4 1">
        3
        2
        1
        0
    </Array>
</LUT1D>

Example 1. Example of a very simple LUT1D

LUT3D

Description:
This node shall contain a 3D LUT in the form of an Array. In a LUT3D, the 3 color components of the input value are used to find the nearest indexed values along each axis of the 3D cube. The 3-component output value is calculated by interpolating within the volume defined by the nearest corresponding positions in the LUT. LUT3Ds have the same dimension on all axes (i.e. Array dimensions are of the form “n n n 3”). A LUT3D with axial dimensions greater than 128x128x128 should be avoided. The scaling of the array values is based on the outBitDepth (the inBitDepth is not considered).

Attributes:

interpolation (optional)

a string indicating the preferred algorithm used to interpolate values in the 3DLUT. This attribute is optional with a default of "trilinear" if the attribute is not present.
Supported values are:

• "trilinear": perform trilinear interpolation
• "tetrahedral": perform tetrahedral interpolation

Note

Interpolation methods are specified in Appendix A.

Elements:

Array (required)

an array of numeric values that are the output values of the 3D LUT. The Array shall contain the table entries for the LUT3D from the minimum to the maximum input values, with the third component index changing fastest.

Attributes:

dim (required)

four integers that reperesent the dimensions of the 3D LUT and the number of color components. The first three values define the dimensions of the LUT and if multiplied shall equal the number of entries actually present in the array. The fourth value indicates the number of components per entry.
4 entries have the dimensions of a 3D cube plus the number of components per entry.

Example

dim = "17 17 17 3" indicates a 17-cubed 3D lookup table with 3 component color

Note

Array is formatted differently when it is contained in a LUT1D or Matrix element (see Array).

Examples:

<LUT3D id="lut-24" name="green look" interpolation="trilinear" inBitDepth="12i" outBitDepth="16f">
    <Description>3D LUT</Description>
    <Array dim="2 2 2 3">
        0.0 0.0 0.0
        0.0 0.0 1.0
        0.0 1.0 0.0
        0.0 1.0 1.0
        1.0 0.0 0.0
        1.0 0.0 1.0
        1.0 1.0 0.0
        1.0 1.0 1.0
    </Array>
</LUT3D>

Example 2. Example of a simple LUT3D

Matrix

Description:
This node specifies a matrix transformation to be applied to the input values. The input and output of a Matrix are always 3-component values.

All matrix calculations should be performed in floating point, and input bit depths of integer type should be treated as scaled floats. If the input bit depth and output bit depth do not match, the coefficients in the matrix must incorporate the results of the ‘scale’ factor that will convert the input bit depth to the output bit depth (e.g. input of 10i with an output of 12i requires the matrix coefficients already have a factor of \(4095/1023\) applied). Changing the input or output bit depth requires creation of a new set of coefficients for the matrix.

The output values are calculated using row-order convention:

\[ \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \begin{bmatrix} r_1\\ g_1\\ b_1 \end{bmatrix} = \begin{bmatrix} r_2\\ g_2\\ b_2 \end{bmatrix} \]

which is equivalent in functionality to the following:

\[ \begin{aligned} r_2 = (r_1 \cdot a_{11}) + (g_1 \cdot a_{12}) + (b_1 \cdot a_{13}) \\ g_2 = (r_1 \cdot a_{21}) + (g_1 \cdot a_{22}) + (b_1 \cdot a_{23}) \\ b_2 = (r_1 \cdot a_{31}) + (g_1 \cdot a_{32}) + (b_1 \cdot a_{33}) \end{aligned} \]

Matrices using an offset calculation will have one more column than rows. An offset matrix may be defined using a 3x4 Array, wherein the fourth column is used to specify offset terms, \(k_1\), \(k_2\), \(k_3\):

\[ \begin{bmatrix} a_{11} & a_{12} & a_{13} & k_1\\ a_{21} & a_{22} & a_{23} & k_2\\ a_{31} & a_{32} & a_{33} & k_3\\ \end{bmatrix} \begin{bmatrix} r_1\\ g_1\\ b_1\\ 1.0 \end{bmatrix} = \begin{bmatrix} r_2\\ g_2\\ b_2 \end{bmatrix} \]

Expanded out, this means that the offset terms \(k_1\), \(k_2\), and \(k_3\) are added to each of the normal matrix calculations:

\[ \begin{aligned} r_2 = (r_1 \cdot a_{11}) + (g_1 \cdot a_{12}) + (b_1 \cdot a_{13}) + k_1\\ g_2 = (r_1 \cdot a_{21}) + (g_1 \cdot a_{22}) + (b_1 \cdot a_{23}) + k_2\\ b_2 = (r_1 \cdot a_{31}) + (g_1 \cdot a_{32}) + (b_1 \cdot a_{33}) + k_3 \end{aligned} \]

Elements:

Array (required)

a table that provides the coefficients of the transformation matrix. The matrix dimensions are either 3x3 or 3x4. The matrix is serialized row by row from top to bottom and from left to right,
i.e., "\(a_{11}\ a_{12}\ a_{13}\ a_{21}\ a_{22}\ a_{23}\ \ldots\)" for a 3x3 matrix.

\[ \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \]

Attributes:

dim (required)

two integers that describe the dimensions of the matrix array. The first value define the number of rows and the second is the number of columns.
2 entries have the dimensions of a matrix

Example

dim = "3 3" indicates a 3x3 matrix

Example

dim = "3 4" indicates a 3x4 matrix

Note

Previous versions of this specification used three integers for the dim attribute, rather than the current two. In order to facilitate backwards compatibility, implementations should allow a third value for the dim attribute and may simply ignore it.

Note

Array is formatted differently when it is contained in a LUT1D or LUT3D element (see Array)

Examples:

<Matrix id="lut-28" name="AP0 to AP1" inBitDepth="16f" outBitDepth="16f" >
    <Description>3x3 color space conversion from AP0 to AP1</Description>
    <Array dim="3 3">
         1.45143931614567     -0.236510746893740    -0.214928569251925
        -0.0765537733960204    1.17622969983357     -0.0996759264375522
         0.00831614842569772  -0.00603244979102103   0.997716301365324
    </Array>
</Matrix>

Example 3. Example of a Matrix node with dim="3 3 3"

<Matrix id="lut-25" name="colorspace conversion" inBitDepth="10i" outBitDepth="10i" >
    <Description> 3x4 Matrix , 4th column is offset </Description>
    <Array dim="3 4">
        1.2     0.0     0.0     0.002
        0.0     1.03    0.001   -0.005
        0.004   -0.007  1.004   0.0
    </Array>
</Matrix>

Example 4. Example of a Matrix node

Range

Description:
This node maps the input domain to the output range by scaling and offsetting values. The Range element can also be used to clamp values.

Unless otherwise specified, the node’s default behavior is to scale and offset with clamping. If clamping is not desired, the style attribute can be set to "noClamp".

To achieve scale and/or offset of values, all of minInValue, minOutValue, maxInValue, and maxOutValue must be present. In this explicit case, the formula for Range shall be:

\[ out = in \times scale + \texttt{minOutValue} - \texttt{minInValue} \times scale \]

where:

\(scale = \dfrac{(\texttt{maxOutValue} - \texttt{minOutValue})}{(\texttt{maxInValue} - \texttt{minInValue})}\)

The scaling of minInValue and maxInValue depends on the input bit-depth, and the scaling of minOutValue and maxOutValue depends on the output bit-depth.

If style="Clamp", the output value of \(out\) from the above equation is furthur modified as follows:

\[ out_{clamped} = \mathrm{MIN}(\texttt{maxOutValue}, \mathrm{MAX}( \texttt{minOutValue}, out)) \]

where:

\(\mathrm{MAX}(a,b)\) returns \(a\) if \(a > b\) and \(b\) if \(b \geq a\)
\(\mathrm{MIN}(a,b)\) returns \(a\) if \(a < b\) and \(b\) if \(b \leq a\)

The Range element can also be used to clamp values on only the top or bottom end. In such instances, no offset is applied, and the formula simplifies because only one pair of min or max values are required. (The style shall not be "noClamp" for this use-case.)

If only the minimum value pair is provided, then the result shall be clamping at the low end, according to:

\[ out = \mathrm{MAX}( \texttt{minOutValue}, in \times bitDepthScale) \]

Values must be set such that \(\texttt{minOutValue} = \texttt{minInValue} \times bitDepthScale\).

Likewise, if only the maximum values pairs are provided, the result shall be clamping at the high end, according to:

\[ out = \mathrm{MIN}( \texttt{maxOutValue}, in \times bitDepthScale) \]

And values must be set such that \(\texttt{maxOutValue} = \texttt{maxInValue} \times bitDepthScale\).

The following formulas are used in the above equations:

\[ bitDepthScale = \dfrac{\mathrm{scaleFactor}(\texttt{outBitDepth})}{\mathrm{scaleFactor}(\texttt{inBitDepth})} \]

\[ \mathrm{scaleFactor}(a) = \begin{cases} 2^{bitDepth}-1 & \text{when }a \in \{\texttt{"8i"},\texttt{"10i"},\texttt{"12i"},\texttt{"16i"}\} \\ 1.0 & \text{when }a \in \{\texttt{"16f"},\texttt{"32f"}\} \end{cases} \]

Note

The bit depth scale factor intentionally uses \(2^{bitDepth}−1\) and not \(2^{bitDepth}\). This means that the scale factor created for scaling between different bit depths is "non-integer" and is slightly different depending on the bit depths being scaled between. While instinct might be that this scale should be a clean bit-shift factor (i.e. \(2\times\) or \(4\times\) scale), testing with a few example values plugged into the formula will show that the resulting non-integer scale is the correct and intended behavior.

At least one pair of either minimum or maximum values, or all four values, must be provided.

Elements:

minInValue (optional)

The minimum input value. Required if minOutValue is present.

maxInValue (optional)

The maximum input value. Required if maxOutValue is present.
The maxInValue shall be greater than the minInValue.

minOutValue (optional)

The minimum output value. Required if minInValue is present.

maxOutValue (optional)

The maximum output value. Required if maxInValue is present.
The maxOutValue shall be greater than or equal to the minOutValue.

Attributes:

style (optional)

Describes the preferred handling of the scaling calculation of the Range node. If the style attribute is not present, clamping is performed.
The options for style are:

"noClamp"

If present, scale and offset is applied without clamping (i.e. values below minOutValue or above maxOutValue are preserved)

"Clamp"

If present, clamping is applied upon the result of the scale and offset expressed by the result of the non-clamping Range equation

Examples:

<Range inBitDepth="10i" outBitDepth="10i">
    <Description>10-bit full range to SMPTE range</Description>
    <minInValue>0</minInValue>
    <maxInValue>1023</maxInValue>
    <minOutValue>64</minOutValue>
    <maxOutValue>940</maxOutValue>
</Range>

Example 5. Using "Range" for scaling 10-bit full range to 10-bit SMPTE (legal) range.

Log

Description:
This node contains parameters for processing pixels through a logarithmic or anti-logarithmic function. A couple of main formulations are supported. The most basic formula follows a pure logarithm or anti-logarithm of either base 2 or base 10. Another supported formula allows for a logarithmic function with a gain factor and offset. This formulation can be used to convert from linear to Cineon. Another style of log formula follows a piece-wise function consisting of a logarithmic function with a gain factor, an offset, and a linear segment. This style can be used to implement many common “camera-log” encodings.

Note

The equations for the Log node assume integer data is normalized to floating-point scaling. LogParams do not change based on the input and output bit-depths.

Note

On occasion it may be necessary to transform a logarithmic function specified in terms of traditional Cineon-style parameters to the parameters used by CLF. Guidance on how to do this is provided in Appendix B.

Attributes:

style (required)

specifies the form of the of log function to be applied
Supported values for ”style” are:

• "log10"
• "antiLog10"
• "log2"
• "antiLog2"
• "linToLog"
• "logToLin"
• "cameraLinToLog"
• "cameraLogToLin"

The formula to be applied for each style is described by the equations below, for all of which:

\[ \texttt{FLT_MIN} = 1.175494 \times 10^{-38} \]

\(\textrm{MAX}(a, b)\) returns \(a\) if \(a \gt b\) and \(b\) if \(b \geq a\)

• "log10": applies a base 10 logarithm according to

\[ y = log_{10}(\textrm{MAX}(x,\texttt{FLT_MIN})) \]

• "antiLog10": applies a base 10 anti-logarithm according to

\[ x = 10^{y} \]

• "log2": applies a base 2 logarithm according to

\[ y = log_{2}(\textrm{MAX}(x,\texttt{FLT_MIN})) \]

• "antiLog2": applies a base 2 anti-logarithm according to

\[ x = 2^{y} \]

• "linToLog": applies a logarithm according to

\[ y = \text{logSideSlope} \times \text{log}_\text{base}(\textrm{MAX}(\text{linSideSlope} \times x + \text{linSideOffset}, \texttt{FLT_MIN}))+\text{logSideOffset} \]

• "logToLin": applies an anti-logarithm according to

\[ x = \frac{\left(\text{base}^{\frac{y-\text{logSideOffset}}{\text{logSideSlope}}} - \text{linSideOffset}\right)}{\text{linSideSlope}} \]

• "cameraLinToLog": applies a piecewise function with logarithmic and linear segments on linear values, converting them to non-linear values

\[ y = \begin{cases} \text{linearSlope} \times x + \text{linearOffset} & \text{if } x \leq \text{linSideBreak}\\ \text{logSideSlope} \times \text{log}_{\text{base}}(\mathrm{MAX}(\text{linSideSlope} \times x + \text{linSideOffset},\texttt{FLT_MIN})) + \text{logSideOffset} & \text{otherwise} \\ \end{cases} \\ \]

Note

The calculation of \(\text{linearSlope}\), and \(\text{linearOffset}\) is described in Solving for LogParams

• "cameraLogToLin": applies a piecewise function with logarithmic and linear segments on non-linear values, converting them to linear values

\[ x = \begin{cases} \frac{(y - \text{linearOffset})}{\text{linearSlope}} & \text{if } y \leq \text{logSideBreak} \\ \frac{\left(\text{base}^{\frac{y-\text{logSideOffset}}{\text{logSideSlope}}} - \text{linSideOffset}\right)}{\text{linSideSlope}} & \text{otherwise} \end{cases} \]

Note

The calculation of \(\text{logSideBreak}\), \(\text{linearSlope}\), and \(\text{linearOffset}\) is described in Solving for LogParams

Elements:

LogParams (required - if "style" is not a basic logarithm)

contains the attributes that control the "linToLog", "logToLin", "cameraLinToLog", or "cameraLogToLin" functions
This element is required if style is of type "linToLog", "logToLin", "cameraLinToLog", or "cameraLogToLin".
Attributes:

"base" (optional)

the base of the logarithmic function
Default is 2.

"logSideSlope" (optional)

"slope" (or gain) applied to the log side of the logarithmic segment.
Default is 1.

"logSideOffset" (optional)

offset applied to the log side of the logarithmic segment.
Default is 0.

"linSideSlope" (optional)

slope of the linear side of the logarithmic segment.
Default is 1.

"linSideOffset" (optional)

offset applied to the linear side of the logarithmic segment.
Default is 0.

"linSideBreak" (optional)

the break-point, defined in linear space, at which the piece-wise function transitions between the logarithmic and linear segments.
This is required if style="cameraLinToLog" or "cameraLogToLin"

"linearSlope" (optional)

the slope of the linear segment of the piecewise function. This attribute does not need to be provided unless the formula being implemented requires it. The default is to calculate using linSideBreak such that the linear portion is continuous in value with the logarithmic portion of the curve, by using the value of the logarithmic portion of the curve at the break-point. This is described in the following note below.

"channel" (optional)

the color channel to which the exponential function is applied. Possible values are "R", "G", "B". If this attribute is utilized to target different adjustments per channel, then up to three LogParams elements may be used, provided that "channel" is set differently in each. However, the same value of base must be used for all channels. If this attribute is not otherwise specified, the logarithmic function is applied identically to all three color channels.

Solving for LogParams

\(\text{linearOffset}\) is the offset of the linear segment of the piecewise function. This value is calculated using the position of the break-point and the linear slope in order to ensure continuity of the two segments. The following steps describe how to calculate \(\text{linearOffset}\).

First, the value of the break-point on the log-axis is calculated using the value of \(\text{linSideBreak}\) as input to the logarithmic segment of the piecewise function, as below:

\[ \text{logSideBreak} = \text{logSideSlope} × \text{log}_{base}(\text{linSideSlope} × \textbf{linSideBreak} + \text{linSideOffset}) + \text{logSideOffset} \]

Then, if \(\text{linearSlope}\) was not provided, the value of \(\text{linSideBreak}\) is used again to solve for the derivative of the logarithmic function. The value of \(\text{linearSlope}\) is set to equal the instantaneous slope at the break-point, or derivative, as shown below:

\[ \text{linearSlope} = \text{logSideSlope} \times \left(\frac{\text{linSideSlope}}{(\text{linSideSlope} \times \textbf{linSideBreak} + \text{linSideOffset}) \times \text{ln}(\text{base})}\right) \]

Finally, the value of \(\text{linearOffset}\) can be solved for by rearranging the linear segment of of the piecewise function and using the values of \(\text{logSideBreak}\) and \(\text{linearSlope}\), as below:

\[ \text{linearOffset} = \textbf{logSideBreak} - \textbf{ linearSlope} \times \text{linSideBreak} \]

Examples:

<Log inBitDepth="16f" outBitDepth="16f" style="log10"> 
    <Description>Base 10 Logarithm</Description>
</Log>

Example 6. Log node applying a base 10 logarithm.

<Log inBitDepth="32f" outBitDepth="32f" style="cameraLinToLog">
    <Description>Linear to DJI D-Log</Description>
    <LogParams base="10" logSideSlope="0.256663" logSideOffset="0.584555"
        linSideSlope="0.9892" linSideOffset="0.0108" linSideBreak="0.0078"
        linearSlope="6.025"/>
</Log>

Example 7. Log node applying the DJI D-Log formula.

Exponent

Description: This node contains parameters for processing pixels through a power law function. Two main formulations are supported. The first follows a pure power law. The second is a piecewise function that follows a power function for larger values and has a linear segment that is followed for small and negative values. The latter formulation can be used to represent the Rec. 709, sRGB, and CIE L* equations.

Attributes:

style (required)

specifies the form of the exponential function to be applied. Supported values are:

• "basicFwd"
• "basicRev"
• "basicMirrorFwd"
• "basicMirrorRev"
• "basicPassThruFwd"
• "basicPassThruRev"
• "monCurveFwd"
• "monCurveRev"
• "monCurveMirrorFwd"
• "monCurveMirrorRev"

Each of these supported styles are described in detail below, and for all of which the following definitions apply:

\(g =\) exponent
\(k =\) offset
\(\textrm{MAX}(a, b)\) returns \(a\) if \(a \gt b\) and \(b\) if \(b \geq a\)

"basicFwd"

applies a power law using the exponent value specified in the ExponentParams element.
Values less than zero are clamped.

\[ \text{basicFwd}(x) = [\textrm{MAX}(0,x)]^g \]

"basicRev"

applies power law using the exponent value specified in the ExponentParams element.
Values less than zero are clamped.

\[ \text{basicRev}(y) = [\textrm{MAX}(0,y)]^{1/g} \]

"basicMirrorFwd"

applies a basic power law using the exponent value specified in the ExponentParams element for values greater than or equal to zero and mirrors the function for values less than zero (i.e. rotationally symmetric around the origin):

\[ \text{basicMirrorFwd}(x) = \begin{cases} x^{g} & \text{if } x \geq 0 \\ [6pt] -\Big[(-x)^{g}\Big] & \text{otherwise} \end{cases} \]

"basicMirrorRev"

applies a basic power law using the exponent value specified in the ExponentParams element for values greater than or equal to zero and mirrors the function for values less than zero (i.e. rotationally symmetric around the origin):

\[ \text{basicMirrorRev}(y) = \begin{cases} y^{1/g} & \text{if } y \geq 0 \\[6pt] -\Big[(-y)^{1/g}\Big] & \text{otherwise} \end{cases} \]

"basicPassThruFwd"

applies a basic power law using the exponent value specified in the ExponentParams element for values greater than or equal to zero and passes values less than zero unchanged:

\[ \text{basicPassThruFwd}(x) = \begin{cases} x^{g} & \text{if } x \geq 0 \\[6pt] x & \text{otherwise} \end{cases} \]

"basicPassThruRev"

applies a basic power law using the exponent value specified in the ExponentParams element for values greater than or equal to zero and and passes values less than zero un- changed:

\[ \text{basicPassThruRev}(y) = \begin{cases} y^{1/g} & \text{if } y \geq 0 \\[6pt] y & \text{otherwise} \end{cases} \]

"monCurveFwd"

applies a power law function with a linear segment near the origin

\[ \text{monCurveFwd}(x) = \begin{cases} \left( \frac{x\:+\:k}{1\:+\:k} \right)^{g} & \text{if } x \geq xBreak \\[8pt] x\:s & \text{otherwise} \end{cases} \]

where:
\(xBreak = \dfrac{k}{g-1}\)

and, for the \(\text{monCurveFwd}\) (above) and \(\text{monCurveRev}\) (below) equations:
\(s = \left(\dfrac{g-1}{k}\right) \left(\dfrac{k g}{(g-1)(1+k)}\right)^{g}\)

"monCurveRev"

applies a power law function with a linear segment near the origin

\[ \text{monCurveRev}(y) = \begin{cases} (1 + k)\:y^{(1/g)} - k & \text{if } y \geq yBreak \\[8pt] \dfrac{y}{s} & \text{otherwise} \end{cases} \]

where:
\(yBreak = \left(\dfrac{k g}{(g-1)(1+k)}\right)^g\)

"monCurveMirrorFwd"

applies a power law function with a linear segment near the origin and mirrors the function for values less than zero (i.e. rotationally symmetric around the origin):

\[ \text{monCurveMirrorFwd}(x) = \begin{cases} \text{monCurveFwd}(x) & \text{if } x \geq 0 \\[8pt] -[\text{monCurveFwd}(-x)] & \text{otherwise} \end{cases} \]

"monCurveMirrorRev"

applies a power law function with a linear segment near the origin and mirrors the function for values less than zero (i.e. rotationally symmetric around the origin):

\[ \text{monCurveMirrorRev}(y) = \begin{cases} \text{monCurveRev}(y) & \text{if } y \geq 0 \\[8pt] -[\text{monCurveRev}(-y)] & \text{otherwise} \end{cases} \]

Note

The above equations assume that the input and output bit-depths are floating-point. Integer values are normalized to the range \([0.0, 1.0]\).

Elements:

ExponentParams (required)

contains one or more attributes that provide the values to be used by the enclosing Exponent element.
If style is any of the “basic” types, then only exponent is required.
If style is any of the “monCurve” types, then exponent and offset are required.

Attributes:

"exponent" (required)

the power to which the value is to be raised
If style is any of the “monCurve” types, the valid range is \([1.0, 10.0]\). The nominal value is 1.0.

Note

When using a “monCurve” style, a value of 1.0 assigned to exponent could result in a divide-by-zero error. Implementors should protect against this case.

"offset" (optional)

the offset value to use
If offset is used, the enclosing Exponent element’s style attribute must be set to one of the “monCurve” types. Offset is not allowed when style is any of the “basic” types.
The valid range is \([0.0, 0.9]\). The nominal value is 0.0.

Note

If zero is provided as a value for offset, the calculation of \(xBreak\) or \(yBreak\) could result in a divide-by-zero error. Implementors should protect against this case.

"channel" (optional)

the color channel to which the exponential function is applied.
Possible values are "R", "G", "B".
If this attribute is utilized to target different adjustments per channel, up to three ExponentParams elements may be used, provided that "channel" is set differently in each. If this attribute is not otherwise specified, the exponential function is applied identically to all three color channels.

Examples:

<Exponent inBitDepth="32f" outBitDepth="32f" style="basicFwd">
    <Description>Basic 2.2 Gamma</Description>
    <ExponentParams exponent="2.2"/>
</Exponent>

Example 8. Using Exponent node for applying a 2.2 gamma.

<Exponent inBitDepth="32f" outBitDepth="32f" style="monCurveFwd">
    <Description>EOTF (sRGB)</Description>
    <ExponentParams exponent="2.4" offset="0.055" />
</Exponent>

Example 9. Using Exponent node for applying the intended EOTF found in IEC 61966-2-1:1999 (sRGB).

<Exponent inBitDepth="32f" outBitDepth="32f" style="monCurveRev">
    <Description>CIE L*</Description>
    <ExponentParams exponent="3.0" offset="0.16" />
</Exponent>

Example 10. Using Exponent node to apply CIE L* formula.

<Exponent inBitDepth="32f" outBitDepth="32f" style="monCurveRev">
    <Description>Rec. 709 OETF</Description>
    <ExponentParams exponent="2.2222222222222222" offset="0.099" />
</Exponent>

Example 11. Using Exponent node to apply Rec. 709 OETF.

ASC_CDL

Description:
This node processes values according to the American Society of Cinematographers’ Color Decision List (ASC CDL) equations. Color correction using ASC CDL is an industry-wide method of recording and exchanging basic color correction adjustments via parameters that set particular color processing equations.

The ASC CDL equations are designed to work on an input domain of floating-point values of [0 to 1.0] although values greater than 1.0 can be present. The output data may or may not be clamped depending on the processing style used.

If the styleattribute is not specified, the node shall default to "Fwd" - i.e. the classic implementation of the v1.2 ASC-CDL equations.

Note

Equations 4.31-4.34 assume that \(in\) and \(out\) are scaled to normalized floating-point range. If the ASC_CDL node has inBitDepth or outBitDepth that are integer types, then the input or output values must be normalized to or from 0-1 scaling. In other words, the slope, offset, power, and saturation values stored in the ProcessNode do not depend on inBitDepth and outBitDepth; they are always interpreted as if the bit depths were float.

Attributes:

id (optional)

This should match the id attribute of the ColorCorrection element in the ASC CDL XML format.

style

Determines the formula applied by the operator. The valid options are:

`"Fwd"

implementation of v1.2 ASC CDL equation (default)

"Rev"

inverse equation

"FwdNoClamp"

similar to the Fwd equation, but without clamping

"RevNoClamp"

inverse equation, without clamping

The first two implement the math provided in version 1.2 of the ASC CDL specification. The second two omit the clamping step and are intended to provide compatibility with the many applications that take that alternative approach.

Elements:

SOPNode (optional)

The SOPNode is optional, and if present, must contain each of the following sub-elements:

Slope

three decimal values representing the R, G, and B slope values, which is similar to gain, but changes the slope of the transfer function without shifting the black level established by offset
Valid values for slope must be greater than or equal to zero (\(\geq\) 0).
The nominal value is 1.0 for all channels.

Offset

three decimal values representing the R, G, and B offset values, which raise or lower overall brightness of a color component by shifting the transfer function up or down while holding the slope constant
The nominal value is 0.0 for all channels.

Power

three decimal values representing the R, G, and B power values, which change the intermediate shape of the transfer function
Valid values for power must be greater than zero (\(\gt\) 0).
The nominal value is 1.0 for all channels.

SatNode (optional)

The SatNode is optional, but if present, must contain one of the following sub-element:

Saturation

a single decimal value applied to all color channels
Valid values for saturation must be greater than or equal to zero (\(\geq\) 0).
The nominal value is 1.0.

Note

If either element is not specified, values should default to the nominal values for each element. If using the "noClamp" style, the result of the defaulting to the nominal values is a no-op.

Note

The structure of this ProcessNode matches the structure of the XML format described in the v1.2 ASC CDL specification. However, unlike the ASC CDL XML format, there are no alternate spellings allowed for these elements.

The math for style="Fwd" is:

\[ out_{\textrm{SOP}} = \textrm{CLAMP}(in \times \textrm{slope} + \textrm{offset})^{\textrm{power}} \]

\[ \begin{aligned} luma &= 0.2126 \times out_{\textrm{SOP,R}} + 0.7152 \times out_{\textrm{SOP,G}} + 0.0722 \times out_{\textrm{SOP,B}} \\ out &= \textrm{CLAMP}\Big[luma + \textrm{saturation} \times (out_{\textrm{SOP}} − luma)\Big] \end{aligned} \]

Where:
\(\textrm{CLAMP()}\) clamps the argument to \([0,1]\)

The math for style="FwdNoClamp" is the same as for "Fwd" but the two clamp() functions are omitted.
Also, if \((in \times \textrm{slope} + \textrm{offset}) < 0\), then no power function is applied.

The math for style="Rev" is:

\[ \begin{aligned} in_{\textrm{clamp}} &= \mathrm{CLAMP}(in) \\ luma &= 0.2126 \times in_{\textrm{clamp,R}} + 0.7152 \times in_{\textrm{clamp,G}} + 0.0722 \times in_{\textrm{clamp,B}} \\ out_{\textrm{SAT}} &= luma + \frac{(in_{\textrm{clamp}} - luma)}{\textrm{saturation}} \end{aligned} \]

\[ out = \mathrm{CLAMP}\left(\frac{\mathrm{CLAMP}(out_{\textrm{SAT}})^{\frac{1}{\textrm{power}}} - \textrm{offset}}{\textrm{slope}}\right) \\ \]

Where:
\(\textrm{CLAMP()}\) clamps the argument to \([0,1]\)

The math for style="RevNoClamp" is the same as for "Rev" but the \(\textrm{CLAMP}()\) functions are omitted.
Also, if \(out_{\textrm{SAT}} \lt 0\), then no power function is applied.

Examples:

<ASC_CDL id="cc01234" inBitDepth="16f" outBitDepth="16f" style="Fwd">
    <Description>scene 1 exterior look</Description>
    <SOPNode>
        <Slope>1.000000 1.000000 0.900000</Slope>
        <Offset>-0.030000 -0.020000 0.000000</Offset>
        <Power>1.2500000 1.000000 1.000000</Power>
    </SOPNode>
    <SatNode>
        <Saturation>1.700000</Saturation>
    </SatNode>
</ASC_CDL>

Example 12. Example of an ASC_CDL node.

Implementation Notes

Bit Depth

Processing Precision

All processing shall be performed using 32-bit floating-point values. The values of the inBitDepth and outBitDepth attributes shall not affect the quantization of color values.

Note

For some hardware devices, 32-bit float processing might not be possible. In such instances, processing should be performed at the highest precision available. Because CLF permits complex series of discrete operations, CLF LUT files are unlikely to run on hardware devices without some form of pre-processing. Any pre-processing to prepare a CLF for more limited hardware applications should adhere to the processing precision requirements.

Input To and Output From a ProcessList

Applications often support multiple pixel formats (e.g. 8i, 10i, 16f, 32f, etc.). Often the actual pixel format to be processed may not agree with the inBitDepth of the first ProcessNode or the outBitDepth of the last ProcessNode. (Note that the ProcessList element itself does not contain global inBitDepth or outBitDepth attributes.) Therefore, in some cases an application may need to rescale a given ProcessNode to be appropriate for the actual image data being processed.

For example, if the last ProcessNode in a ProcessList is a LUT1D with an outBitDepth of 12i, it indicates that the LUT Array values are scaled relative to 4095. If the application wants to produce floating-point pixel values, it should therefore divide the LUT Array values by 4095 before processing the pixels (according to Conversion). Likewise, if the outBitDepth was instead 32f and the application wants to produce 12i pixel values, it should multiply the LUT Array values by 4095. (Note that in this case, since the result of the computations may exceed 4095 and the application wants to produce 12-bit integer output, the application would want to clamp, round, and quantize the value.)

Input To and Output From a ProcessNode

In order to ensure the scaling of parameter values of all ProcessNodes in a ProcessList are consistent, the inBitDepth of each ProcessNode must match the outBitDepth of the previous ProcessNode (if any).

Please note that an integer inBitDepth or outBitDepth of a ProcessNode does not indicate that any clamping or quantization should be done. These attributes are strictly used to indicate the scaling of parameter and array values. As discussed above, processing precision shall be floating-point.

Furthermore, because the processing precision is intended to be floating-point, the inBitDepth and outBitDepth only control the scaling of parameter and array values and do not impose range limits. For example, even if the outBitDepth of a LUT Array is 12i, it does not mean that the Array values must be limited to \([0,4095]\) or that they must be integer values. It simply means that in order to rescale to 32f that a scale factor of 1/4095 should be used (as per Conversion).

Because processing within a ProcessList should be done at floating-point precision, applications may optionally want to rescale the interfaces all ProcessNodes “interior” to a ProcessList to be 32f according to Conversion. As discussed in Input To and Output From a ProcessList, applications may want to rescale the “exterior” interfaces of the ProcessList based on the type of pixel data being processed.

For some applications, it may be easiest to simply rescale all ProcessNodes to 32f input and output bit-depth when parsing the file. That way, the ProcessList may be considered a purely 32f set of operations and the implementation therefore does not need to track or deal with bit-depth differences at the ProcessNode level.

Conversion Between Integer and Normalized Float Scaling

As discussed above, the inBitDepth or outBitDepth of a ProcessNode may need to be rescaled in order to accommodate the pixel data type being processed by the application.

The scale factor associated with the bit-depths 8i, 10i, 12i, and 16i is \(2^n − 1\), where \(n\) is the bit-depth.

The scale factor associated with the bit-depths 16f and 32f is 1.0.

To rescale Matrix, LUT1D, or LUT3D Array values when the outBitDepth changes, the scale factor is equal to \(\frac{\textrm{newScale}}{\textrm{oldScale}}\). For example, to convert from 12i to 10i, multiply array values by \(1023/4095\).

To rescale Matrix Array values when the inBitDepth changes, the scale factor is equal to \(\frac{\textrm{oldScale}}{\textrm{newScale}}\). For example, to convert from 32f to 10i, multiply array values by \(1/1023\).

To rescale Range parameters when the inBitDepth changes, the scale factor for minInValue and maxInValue is \(\frac{\textrm{newScale}}{\textrm{oldScale}}\). To rescale Range parameters when the outBitDepth changes, the scale factor for minOutValue and maxOutValue is \(\frac{\textrm{newScale}}{\textrm{oldScale}}\).

Please note that in all cases, the conversion shall be only a scale factor. In none of the above cases should clamping or quantization be applied.

Aside from the specific cases listed above, changes to inBitDepth and outBitDepth do not affect the parameter or array values of a given ProcessNode.

If an application needs to convert between different integer pixel formats or between integer and float (or vice versa) on the way into or out of a ProcessList, the same scale factors should be used. Note that when converting from floating-point to integer at the application level that values should be clamped, rounded, and quantized.

Required vs Optional

The required or optional indicated in parentheses throughout this specification indicate the requirement for an element or attribute to be present for a valid CLF file. In the spirit of a LUT format to be used commonly across different software and hardware, none of the elements or attributes should be considered optional for implementors to support. All elements and attributes, if present, should be recognized and supported by an implementation.

If, due to hardware or software limitations, a particular element or attribute is not able to be supported, a warning should be issued to the user of a LUT that contains one of the offending elements. The focus shall be on the user and maintaining utmost compatibility with the specification so that LUTs can be interchanged seamlessly.

Efficient Processing

The transform engine may merge some ProcessNodes in order to obtain better performance. For example, adjacent Matrix operators may be combined into a single matrix. However, in general, combining operators in a way that preserves accuracy is difficult and should be avoided.

Hardware implementations may need to convert all ProcessNodes into some other form that is consistent with what the hardware supports. For example, all ProcessNodes might need to be combined into a single 3D LUT. Using a grid size of 64 or larger is recommended to preserve as much accuracy as possible. Implementors should be aware that the success of such approximations varies greatly with the nature of the input and output color spaces. For example, if the input color space is scene-linear in nature, it may be necessary to use a “shaper LUT” or similar non-linearity before the 3D LUT in order to convert values into a more perceptually uniform representation.

Extensions

It is recommended that implementors of CLF file readers protect against unrecognized elements or attributes that are not defined in this specification. Unrecognized elements that are not children of the Info element should either raise an error or at least provide a warning message to the user to indicate that there is an operator present that is not recognized by the reader. Applications that need to add custom metadata should place it under the Info element rather than at the top level of the ProcessList.

One or more Description elements in the ProcessList can and should be used for metadata that does not fit into a provided field in the Info element and/or is unlikely to be recognized by other applications.

Examples

<?xml version="1.0" encoding="UTF-8"?>
<ProcessList id="ACEScsc.ACES_to_ACEScg.a1.0.3" name="ACES2065-1 to ACEScg" 
    compCLFversion="3.0">
    <Info>
        <ACEStransformID>ACEScsc.ACES_to_ACEScg.a1.0.3</ACEStransformID>
        <ACESuserName>ACES2065-1 to ACEScg</ACESuserName>
    </Info>
    <Description>ACES2065-1 to ACEScg</Description>
    <InputDescriptor>ACES2065-1</InputDescriptor>
    <OutputDescriptor>ACEScg</OutputDescriptor>
    <Matrix inBitDepth="16f" outBitDepth="16f">
        <Array dim="3 3">
             1.451439316146 -0.236510746894 -0.214928569252
            -0.076553773396  1.176229699834 -0.099675926438
             0.008316148426 -0.006032449791  0.997716301365
        </Array>
    </Matrix>
</ProcessList>

Example 13. ACES2065-1 to ACEScg

<?xml version="1.0" encoding="UTF-8"?>
<ProcessList id="ACEScsc.ACES_to_ACEScct.a1.0.3" name="ACES2065-1 to ACEScct" 
    compCLFversion="3.0">
    <Description>ACES2065-1 to ACEScct Log working space</Description>
    <InputDescriptor>Academy Color Encoding Specification (ACES2065-1)</InputDescriptor>
    <OutputDescriptor>ACEScct Log working space</OutputDescriptor>
    <Info>
        <ACEStransformID>ACEScsc.ACES_to_ACEScct.a1.0.3</ACEStransformID>
        <ACESuserName>ACES2065-1 to ACEScct</ACESuserName>
    </Info>
    <Matrix inBitDepth="16f" outBitDepth="16f">
        <Array dim="3 3">
             1.451439316146 -0.236510746894 -0.214928569252
            -0.076553773396  1.176229699834 -0.099675926438
             0.008316148426 -0.006032449791  0.997716301365
        </Array>
    </Matrix>
    <Log inBitDepth="16f" outBitDepth="16f" style="cameraLinToLog">
        <LogParams base="2" logSideSlope="0.05707762557" logSideOffset="0.5547945205" 
            linSideBreak="0.0078125" />
    </Log>
</ProcessList>

Example 14. ACES2065-1 to ACEScct

<?xml version="1.0" encoding="UTF-8"?>
<ProcessList id="5ac02dc7-1e02-4f87-af46-fa5a83d5232d" compCLFversion="3.0">
    <Description>CIE-XYZ D65 to CIELAB L*, a*, b* (scaled by 1/100, neutrals at 
        0.0 chroma)</Description>
    <InputDescriptor>CIE-XYZ, D65 white (scaled [0,1])</InputDescriptor>
    <OutputDescriptor>CIELAB L*, a*, b* (scaled by 1/100, neutrals at 0.0 
        chroma)</OutputDescriptor>
    <Matrix inBitDepth="16f" outBitDepth="16f">
        <Array dim="3 3">
            1.052126639 0.000000000 0.000000000
            0.000000000 1.000000000 0.000000000
            0.000000000 0.000000000 0.918224951
        </Array>
    </Matrix>
    <Exponent inBitDepth="16f" outBitDepth="16f" style="monCurveRev">
        <ExponentParams exponent="3.0" offset="0.16" />
    </Exponent>
    <Matrix inBitDepth="16f" outBitDepth="16f">
        <Array dim="3 3">
            0.00000000  1.00000000  0.00000000
            4.31034483 -4.31034483  0.00000000
            0.00000000  1.72413793 -1.72413793
        </Array>
    </Matrix>
</ProcessList>

Example 15. CIE XYZ to CIELAB

Appendices

Appendix A: Interpolation

When an input value falls between sampled positions in a LUT, the output value must be calculated as a proportion of the distance along some function that connects the nearest surrounding values in the LUT. There are many different types of interpolation possible, but only three types of interpolation are currently specified for use with the Common LUT Format (CLF).

The first interpolation type, linear, is specified for use with a LUT1D node. The other two, trilinear and tetrahedral interpolation, are specified for use with a LUT3D node.

Linear Interpolation

With a table of the sampled input values in \(inValue[i]\) where \(i\) ranges from \(0\) to \((n-1)\), and a table of the corresponding output values in \(outValue[j]\) where \(j\) is equal to \(i\),

index \(i\)	inValue		index \(j\)	outValue
0	0		0	0
\(\vdots\)	\(\vdots\)		\(\vdots\)	\(\vdots\)
\(n - 1\)	1		\(n - 1\)	1000

the \(output\) resulting from \(input\) can be calculated after finding the nearest \(inValue[i] < input\).

When \(inValue[i] = input\), the result is evaluated directly.

\[ output = \dfrac{input-inValue[i]}{inValue[i+1]-inValue[i]} \times (outValue[j+1]-outValue[j])+outValue[j] \]

Trilinear Interpolation

Trilinear interpolation implements linear interpolation in three-dimensions by successively interpolating each direction.

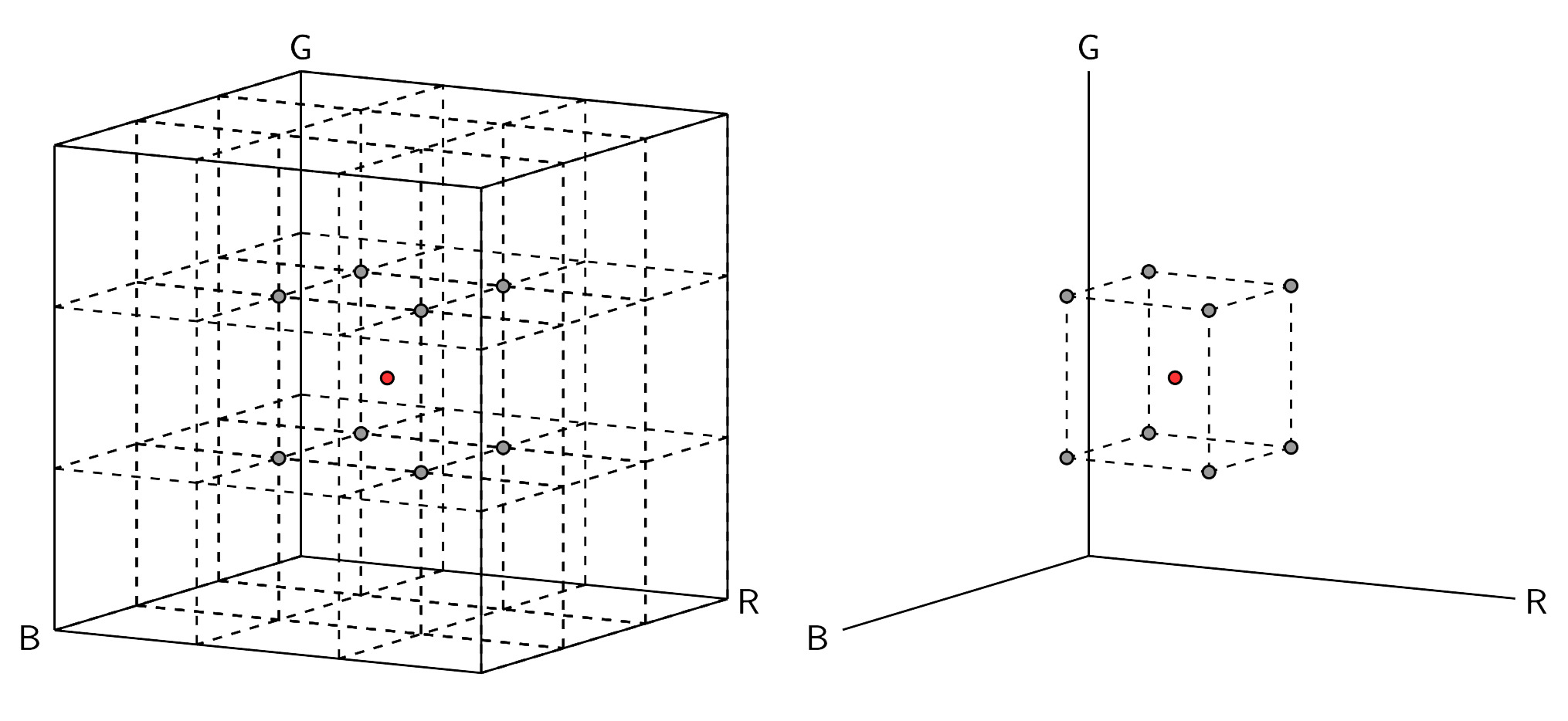
Figure 3 - Illustration of a sampled point located within a basic 3D LUT mesh grid (left) and the same point but with only the vertices surrounding the sampled point (right).

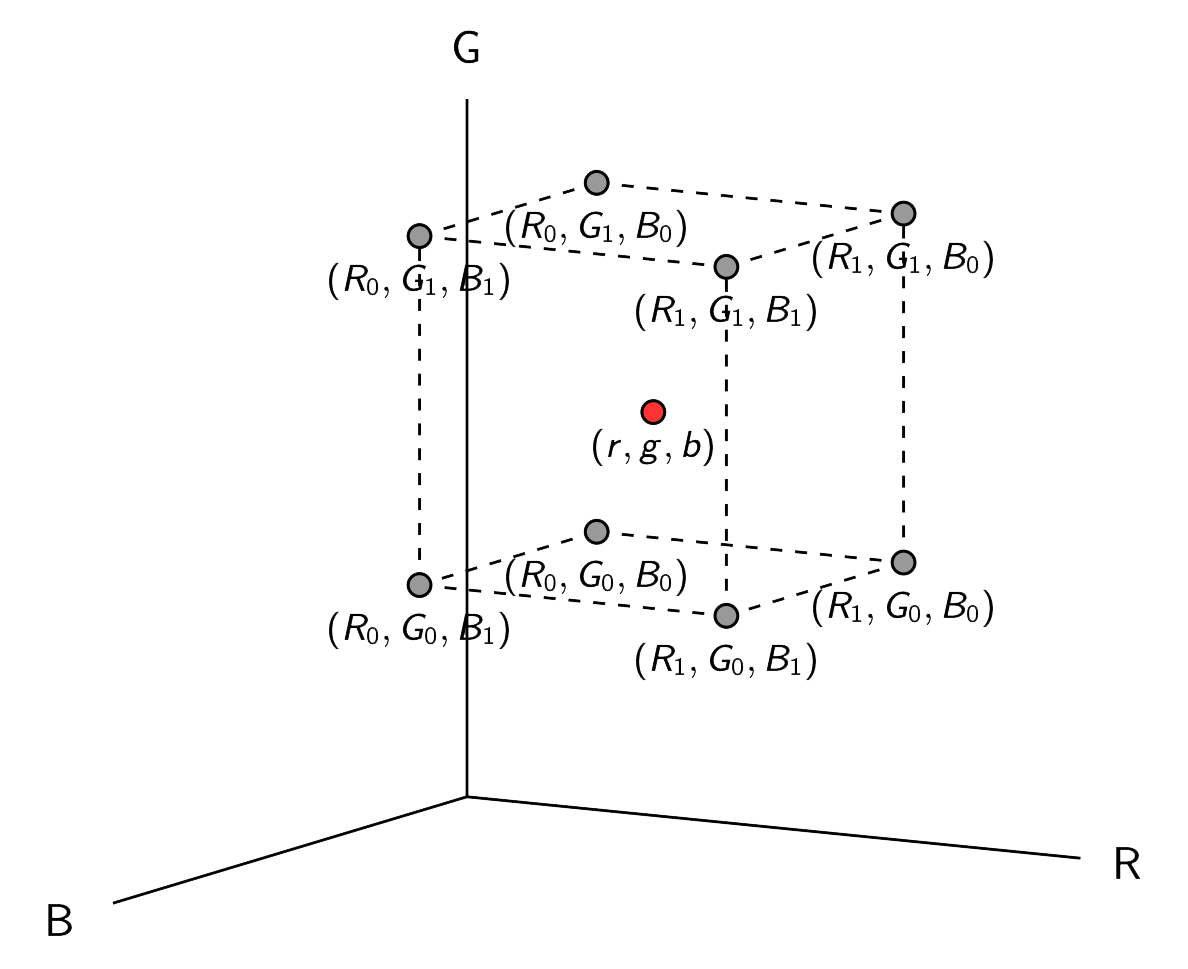
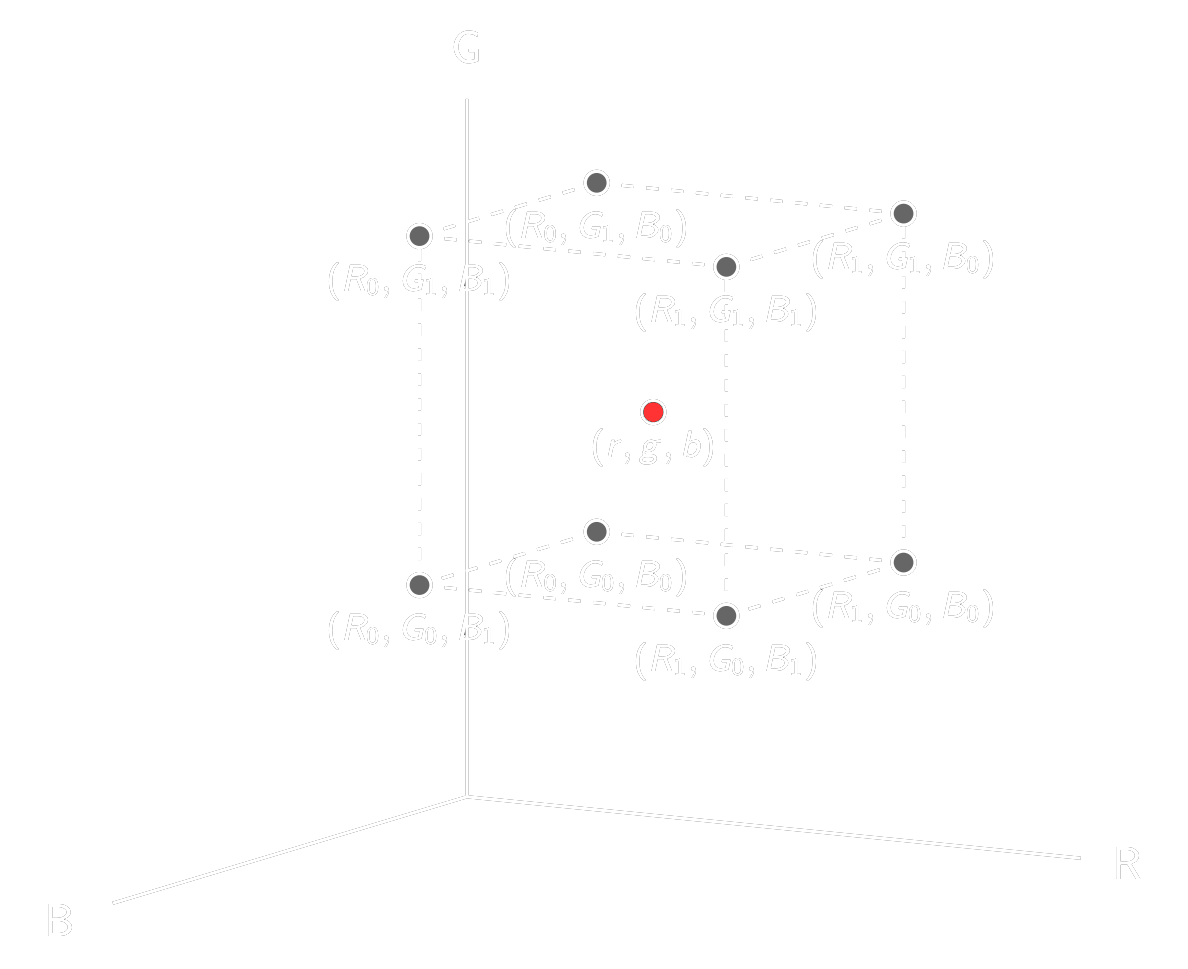
Figure 4 - Labeling the mesh points surrounding the sampled point (r,g,b).

Note

The convention used for notation is uppercase variables for mesh points and lowercase variables for points on the grid.

Consider a sampled point as depicted in Figure 4. Let \(V(r,g,b)\) represent the value at the point with coordinate \((r,g,b)\). The distance between each node per color coordinate shows the proportion of each mesh point's color coordinate values that contribute to the sampled point.

\[ \Delta_r = \frac{r - R_0}{R_1 - R_0} \hspace{0.25in} \Delta_g = \frac{g - G_0}{G_1 - G_0} \hspace{0.25in} \Delta_b = \frac{b - B_0}{B_1 - B_0} \]

The general expression for trilinear interpolation can be expressed as:

\[ V(r,g,b) = c_0 + c_1\Delta_b + c_2\Delta_r + c_3\Delta_g + c_4\Delta_b\Delta_r + c_5\Delta_r\Delta_g + c_6\Delta_g\Delta_b + c_7\Delta_r\Delta_g\Delta_b \]

where:

\[ \begin{aligned} c_0 &= V(R_0, G_0, B_0) \\ c_1 &= V(R_0, G_0, B_1) - V(R_0, G_0, B_0) \\ c_2 &= V(R_1, G_0, B_0) - V(R_0, G_0, B_0) \\ c_3 &= V(R_0, G_1, B_0) - V(R_0, G_0, B_0) \\ c_4 &= V(R_1, G_1, B_1) - V(R_1, G_0, B_0) - V(R_0, G_0, B_1) + V(R_0, G_0, B_0) \\ c_5 &= V(R_1, G_1, B_0) - V(R_0, G_1, B_0) - V(R_1, G_0, B_0) + V(R_0, G_0, B_0) \\ c_6 &= V(R_0, G_1, B_1) - V(R_1, G_1, B_0) - V(R_0, G_0, B_1) + V(R_0, G_0, B_0) \\ c_7 &= V(R_1, G_1, B_1) - V(R_1, G_1, B_0) - V(R_0, G_1, B_1) - V(R_1, G_0, B_1) \\ &+ V(R_0, G_0, B_1) + V(R_0, G_1, B_0) + V(R_1, G_0, B_0) - V(R_0, G_0, B_0) \end{aligned} \]

Expressed in matrix form:

\[ \begin{gather} \mathbf{C} = [c_0 \enspace c_1 \enspace c_2 \enspace c_3 \enspace c_4 \enspace c_5 \enspace c_6 \enspace c_7]^T \\ \mathbf{\Delta} = [1 \quad \Delta_b \quad \Delta_r \quad \Delta_g \quad \Delta_b\Delta_r \quad \Delta_r\Delta_g \quad \Delta_g\Delta_b \quad \Delta_r\Delta_g\Delta_b]^T \\ V(r,g,b) = \mathbf{C}^T \mathbf{\Delta} \end{gather} \]

\[ \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \\ c_7 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ -1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & 0 & -1 & 0 & 1 & 0 \\ 1 & -1 & -1 & 1 & 0 & 0 & 0 & 0 \\ 1 & -1 & 0 & 0 & -1 & 1 & 0 & 0 \\ -1 & 1 & 1 & -1 & 1 & -1 & -1 & 1 \end{bmatrix} \begin{bmatrix} V(R_0, G_0, B_0) \\ V(R_0, G_1, B_0) \\ V(R_1, G_0, B_0) \\ V(R_1, G_1, B_0) \\ V(R_0, G_0, B_1) \\ V(R_0, G_1, B_1) \\ V(R_1, G_0, B_1) \\ V(R_1, G_1, B_1) \end{bmatrix} \]

The expression in above can be written as: \(\mathbf{C} = \mathbf{A}\mathbf{V}\).

Trilinear interpolation shall be done according to \(V(r,g,b) = \mathbf{C}^T \mathbf{\Delta} = \mathbf{V}^T \mathbf{A}^T \mathbf{\Delta}\).

Note

The term \(\mathbf{V}^T \mathbf{A}^T\) does not depend on the variable \((r,g,b)\) and thus can be computed in advance for optimization. Each sub-cube can have the values of the vector \(\mathbf{C}\) already stored in memory. Therefore the algorithm can be summarized as:

1. Find the sub-cube containing the point \((r,g,b)\)
2. Select the vector \(\mathbf{C}\) corresponding to that sub-cube
3. Compute \(\Delta_r\), \(\Delta_g\), \(\Delta_b\)
4. Return \(V(r,g,b) = \mathbf{C}^T \mathbf{\Delta}\)

Tetrahedral Interpolation}

Tetrahedral interpolation subdivides the cubelet defined by the vertices surrounding a sampled point into six tetrahedra by segmenting along the main (and usually neutral) diagonal (Figure 5).

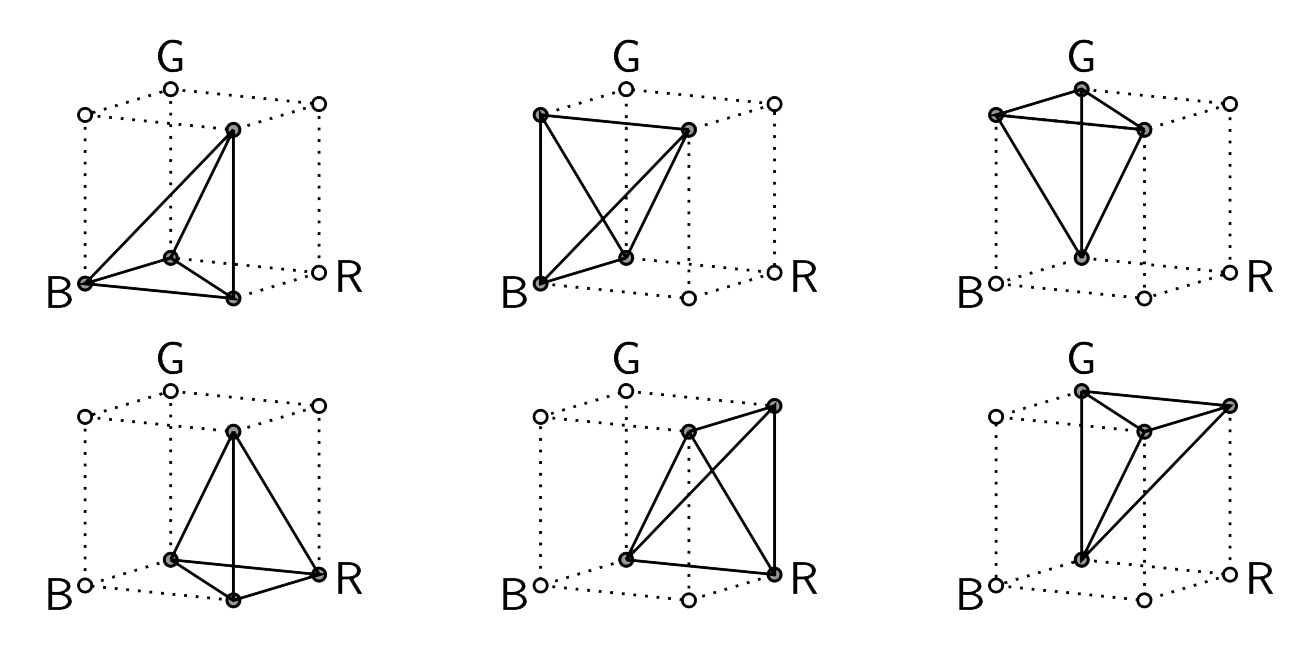
Figure 5 - Illustration of the six subdivided tetrahedra.

To find the tetrahedron containing the point \((r,g,b)\):

• if \(\Delta_b > \Delta_r > \Delta_g\), then use the first tetrahedron, \(t1\)
• if \(\Delta_b > \Delta_g > \Delta_r\), then use the first tetrahedron, \(t2\)
• if \(\Delta_g > \Delta_b > \Delta_r\), then use the first tetrahedron, \(t3\)
• if \(\Delta_r > \Delta_b > \Delta_g\), then use the first tetrahedron, \(t4\)
• if \(\Delta_r > \Delta_g > \Delta_b\), then use the first tetrahedron, \(t5\)
• else, use the sixth tetrahedron, \(t6\)

The matrix notation is:

\[ \mathbf{V} = \begin{bmatrix} V(R_0, G_0, B_0) \\ V(R_0, G_1, B_0) \\ V(R_1, G_0, B_0) \\ V(R_1, G_1, B_0) \\ V(R_0, G_0, B_1) \\ V(R_0, G_1, B_1) \\ V(R_1, G_0, B_1) \\ V(R_1, G_1, B_1) \end{bmatrix}\\ \\ \]

\[ \mathbf{\Delta_t} = [1 \enspace \Delta_b \enspace \Delta_r \enspace \Delta_g]^T \]

\[ \begin{aligned} \mathbf{T}_1 = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 \end{bmatrix} \hspace{0.5in} \mathbf{T}_2 = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 0 & 1 \\ 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0 \end{bmatrix} \\ \mathbf{T}_3 = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 0 & 1 \\ -1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \hspace{0.5in} \mathbf{T}_4 = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 & 0 & 1 & 0 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 \end{bmatrix} \\ \mathbf{T}_5 = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 0 & 0 & 1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 1 & 0 & 0 & 0 & 0 \end{bmatrix} \hspace{0.5in} \mathbf{T}_6 = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 0 & 0 & 1 \\ 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 \\ -1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{aligned} \]

Trilinear interpolation shall be done according to:

\[ \begin{gather} V(r,g,b)_{t1} = \mathbf{\Delta}^T_t \mathbf{T}_1 \mathbf{V}\\ V(r,g,b)_{t2} = \mathbf{\Delta}^T_t \mathbf{T}_2 \mathbf{V}\\ V(r,g,b)_{t3} = \mathbf{\Delta}^T_t \mathbf{T}_3 \mathbf{V}\\ V(r,g,b)_{t4} = \mathbf{\Delta}^T_t \mathbf{T}_4 \mathbf{V}\\ V(r,g,b)_{t5} = \mathbf{\Delta}^T_t \mathbf{T}_5 \mathbf{V}\\ V(r,g,b)_{t6} = \mathbf{\Delta}^T_t \mathbf{T}_6 \mathbf{V} \end{gather} \]

Note

The vectors \(\mathbf{T}_i \mathbf{V}\) for \(i = 1,2,3,4,5,6\) does not depend on the variable \((r,g,b)\) and thus can be computed in advance for optimization.

Appendix B: Cineon-style Log Parameters

When using a Log node, it might be desirable to conform an existing logarithmic function that uses Cineon style parameters to the parameters used by CLF. A translation from Cineon-style parameters to those used by CLF's LogParams element is quite straightforward using the following steps.

Traditionally, \(\textrm{refWhite}\) and \(\textrm{refBlack}\) are provided as 10-bit quantities, and if they indeed are, first normalize them to floating point by dividing by 1023:

\[ \begin{align} \textrm{refWhite} = \frac{\textrm{refWhite}_{10i}}{1023.0} \\[12pt] \textrm{refBlack} = \frac{\textrm{refBlack}_{10i}}{1023.0} \end{align} \]

where subscript 10\(i\) indicates a 10-bit quantity.

The density range is assumed to be:

\[ \textrm{range} = 0.002 \times 1023.0 \]

Then solve the following quantities:

\[ \begin{align} \textrm{multFactor} =& \frac{\textrm{range}}{\textrm{gamma}} \\ \textrm{gain} =& \frac{\textrm{highlight} - \textrm{shadow}}{1.0 - 10^{( MIN( \textrm{multFactor} \times (\textrm{refBlack}-\textrm{refWhite}), -0.0001)}} \\[6pt] \textrm{offset} =& \ \textrm{gain} - (\textrm{highlight} - \textrm{shadow}) \\ \end{align} \]

Where \(MIN(x,y)\) returns \(x\) if \(x<y\), otherwise returns \(y\)

The parameters for the LogParams element are then:

\[\begin{align} \texttt{base} =& \ 10.0 \\[6pt] \texttt{logSlope} =& \ \frac{1}{\textrm{multFactor}} \\[6pt] \texttt{logOffset} =& \ \textrm{refWhite} \\[6pt] \texttt{linSlope} =& \ \frac{1}{\textrm{gain}} \\[6pt] \texttt{linOffset} =& \ \frac{\textrm{offset}-\textrm{shadow}}{\textrm{gain}} \end{align}\]

Appendix C: Changes between v2.0 and v3.0

• Add Log ProcessNode
• Add Exponent ProcessNode
• Revise formulas for defining use of Range ProcessNode to clamp at the low or high end.
• IndexMaps removed. Use a halfDomain LUT to achieve reshaping of input to a LUT.
• Move ACEStransform elements to Info element of ProcessList in main spec
• Changed syntax for dim attribute of Array when contained in a Matrix. Two integers are now used to define the dimensions of the matrix instead of the previous three values which defined the dimensions of the matrix and the number of color components.